Mapping a Square to a Circle

I wanted to come up with a nice way to map all the points in the square



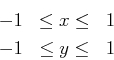
to the points in the unit circle, such that the points along the axes are unchanged, and the corners get normalized. The way I went about this was to think of a line of constant x (as well as a line of constant y) getting mapped to an ellipse in the circle. So for our first requirement to hold true, the ellipse for some constant x has the equation



Now we want to make sure that points along the curve at the top of the circle (from 45 degrees to 135 degrees) are all accounted for. So for x between -1 and 1, we want the ellipse to pass through the point



So we'll plug that in, and that should give us the b coefficient for our ellipse



So the ellipse for constant x is



Similarly, for a line of constant y, we get the ellipse



Solving the first for x', we get



Plugging this into the second equation gives



and by symmetry we can see that the mapping



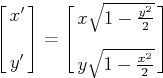
takes the square from -1 to 1 on the x and y axes, to the unit circle. Here's a demonstration of that mapping, which shows its effect on various grid lines.



I'd like to find a way to map a cube to the unit sphere. Hopefully I can get that ready for the next post.