Smoothing a Sequence of Points (Part 2)

This is the second part of a method to smooth out sequences of points such that they maintain their rough shape, but loose all the high frequency noise. Refer to Part 1 for definitions and background.

The second special case we'll consider is a zig-zag pattern, where the angle between consecutive points is always the same, the distance is consistent, and all the points are coplanar.



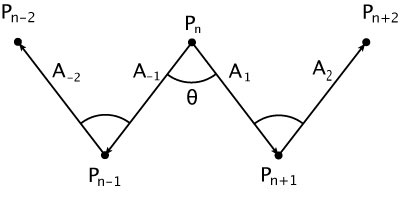
The desired result is that a sequence of points like this will get flattened out to a straight line in a single application of the filter.



This can be accomplished if



Using this fact along with the constraint from Part 1 that



gives us



Here's a couple of demos that show the effects of this filter over 30 iterations. Each point alternates in color from blue to red, so that you can see the concentration of points along the line list. The first is like the points generated from a character swinging a weapon around in a circle, with infrequent samples. If you lay down 4 or 5 points per sample (along the straight lines between the samples), and then apply the filter, you'll get results like this



The next example is more of a noisy data set, and you can see how the noise gets eliminated, but the general shape is preserved.



So finally, the filter that accomplishes both of our goals is