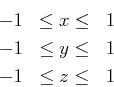
to the points in the unit sphere. In the last post I used the mapping

Taking the length of the new point gives

So you can see that if x or y are either -1 or +1, this yeilds a vector with unit length. So, beginning with this, I decided that I'd work backward from the guess that if I had a mapping from the cube to the unit sphere, the length of a generated point would need to be
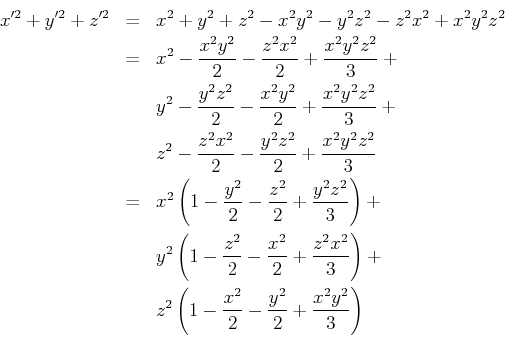
Which leads to the mapping
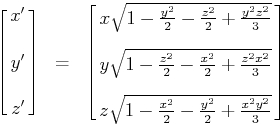
Trying this out yields some pretty nice results. This is the cube and its mapping onto the unit sphere. The thick lines are lines where at least two of the components are -1 or +1.
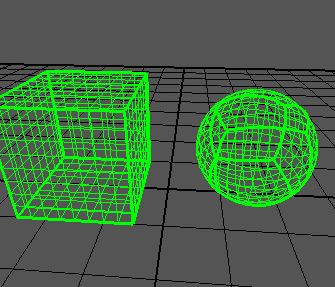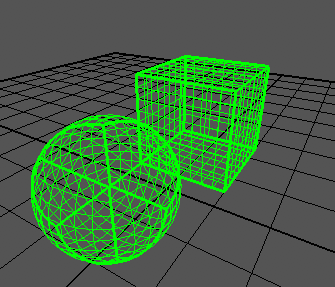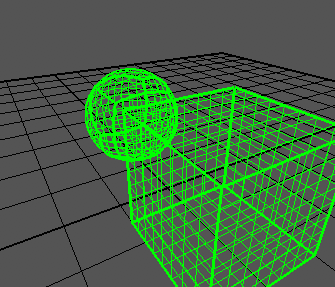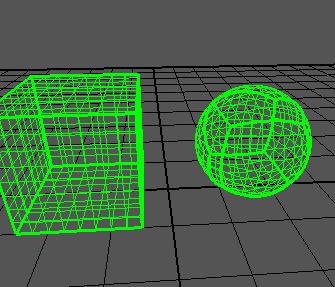
And here's another view from inside the sphere

Sorry this post is a little light on justification. I might try to explain this by looking at the level curves defined by constant x, y and z, but I'll save that for another day (maybe).
wow, didn't sphere mapping could be done that way. Sw33t!!!!
ReplyDeleteNice, but an inverse transform would be nice. How do you take coordinates on the sphere and transform them to coordinates on the cube?
ReplyDeleteI've been working on it for a few minutes, but the algebra gets a little messy ;)
That is very elegant - I like it!
ReplyDeleteInverse transform would be nice idd !!!
ReplyDeleteI would also love to see an inverse of this transformation.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeletePlease could you tell me inverse transformation - thx
ReplyDeletethe_andreyp@hotmail.com
thx )
nice job..inverse transformation would be great
ReplyDeleteHave you got any idea the transformations between that cube sphere you have and a conventional longitude/ latitude model?
ReplyDeleteJust a random comment - shouldn't the view from inside the sphere, at its very center - look exactly as if you were inside the cube?
ReplyDeleteI've posted a solution for the reverse mapping from sphere to cube on my blog: http://petrocket.blogspot.com/2010/04/sphere-to-cube-mapping.html
ReplyDeleteI also did a reverse mapping for the 2D version if anyone wants that.
Thank you :) Saved me a lot of time and effort
ReplyDeleteWow really loved the formula, Have you worked on transferring rectangular cube to ellipsoid? same thing for your previous post. How to transfer from rectangle to ellipse?
ReplyDeleteWould you please email me if you have the answer?
Thanks
Answering the question posed by Anonymous above:
ReplyDeleteLet V be a vector from the center to a point on the sphere.
Take the greatest of the 3 coordinates and use it to decide which face of the cube you're onto. For instance (1, 0, 0) means positive-X side of the cube.
Use the other two coordinates as planar 2D coordinates within that face.
(see cubic environment mapping)
This is very useful. Thank you.
ReplyDeleteNice work man!
ReplyDeleteYou are Genious!!! Good work.
ReplyDeleteAmazing! That's exactly what I'm looking for!
ReplyDeleteCould you help me out with this but going from sphere mapping to cube? I want to use a panoramic texture in a cube environment.
ReplyDeleteMaik
Very interesting indeed. Could you be so kind as to post the mapping of a sphere to a rectangular prism having sides A, B, and C? That would be very useful to me.
ReplyDelete