Smoothing a Sequence of Points (Part 1)

The problem came up of rendering a ribbon and making sure that the points used for the ribbon are nice and smooth. This list of points is generated from an animated object that moves and rotates quickly, and sampling the animation tends to give really jagged results. One solution is to evaluate the animation multiple times per frame to get extra samples to smooth the ribbon out. This seems a little costly, so I wanted to figure out if there was some way to smooth out the ribbon without having to do extra animation updates.

Let's call the nth point in the point sequence P_n. Also (for convenience) let's define





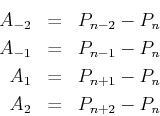
We'll try to smooth out this point sequence by applying a filter to each point in the sequence that adds in bits of nearby points to try to smooth out the sequence.

Note that specifying a filter as the sum of coefficients on the points P_n-2 through P_n+2 requires that all the coefficients add up to 1 (otherwize the filter will yield different results depending on where P_n is relative to the origin). Using coefficients on the A_i vectors and the P_n point, the requirement is that the coefficient on P_n is 1 and the coefficients on the A_i vectors can be whatever we want.

The first idea that came to mind to shave off sharp corners was to calculate the filtered P_n (call it P'_n) as a weighted average of P_n and the midpoint between P_n-1 and P_n+1.



Not only would this flatten out sharp corners, but it also takes a non-uniformly distributed sequence of collinear points, and (after a number of iterations) distributes them evenly along the line. In terms of the A_i we get



This filter, however, tends to either flatten out curves quickly (for values of a close to zero), or not have much effect (for values of a close to one). So I thought it might be worthwhile to introduce A_-2 and A₂ multiplied by a coefficient b, and then subtract that sum from the previous filter. The idea is to try to push out points on a smooth curve that would otherwise get flattened, while still allowing more high frequency noise to get flattened out.

Over the next few weeks we'll consider two uniform cases, and try to find coefficients a and b that will accomplish these goals. The case that we'll consider this week is one of constant curvature, where the distance between each pair of consecutive points is the same, the angles formed between P_n-1, P_n and P_n+1 is consistant, and all the points are coplanar.



Its easy to see that these points fall on a circle, and a vector toward the center of the circle (from P_n) is (A_-1 + A₁). So to measure whether a filter will shrink or grow one of these point sequences, we just need to check the sign of


Equation (1)


Setting this to zero and solving for b gives


Equation (2)


Given a particular θ and a particular a, this tells us what b will provide a root of equation (1). Also, we can see that for any θ from π/3 to π, cos θ + cos 2 θ < 0. So in this range (1) increases as b increases. For θ from 0 to π/3, cos θ + cos 2 θ > 0, so equation (1) increases as b decreases.


Graph of Equation (2) for a = 0.5 with extrema at 0 and π


Therefore the allowable range of values for b is bounded below by the maximum for (2) with θ in the range 0 to π/3, and above by the minimum of (2) with θ in the range π/3 to π. So to find these extrema of (2), we'll take it's derivative, and set it equal to zero.



This equals zero where sin θ = 0. And so the extrema are at θ = 0 and π. These extrema give the range



This maximum ((1-a)/6) turns out to work very well. We haven't really proven anything about filtering general 3D point sequences, but this line of reasoning can be used on the 2D projections of 3D curves, and its pretty easy to see that the 2D projection of a filtered sequence is the same as filtering the 2D projection of the original sequence. We'll leave it for next week to pursue this subject further and come up with another constraint in order to decide on a pair of values for a and b that will accomplish another desirable effect.