Nth Term of the Fibonacci Sequence

I can't remember how I first found this proof .. I think it might have been a homework assignment. Regardless, it's been one of my favorite proofs ever since, so I figured I should probably include it here. The object is to come up with a closed form solution for the nth term of the Fibonacci sequence f={0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...} (I start with zero for the zeroth fibonacci number, and one for the first, but you'll see that this method allows you to easily compute a Fibonacci-like sequence with any two initial values)

Now lets write an iterative formula for the nth and (n+1)th term, and then we'll solve for a closed form solution.



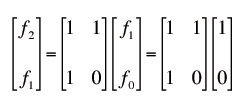
So you can see, by multiplying this matrix repeatedly, it yields the nth and (n+1)th term



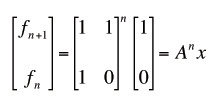
Now to simplify that nasty nth power of A, we'll use a trick known as diagonalization. If we can write A as a product of 3 matrices P, D and P inverse, where D is a diagonal matrix, it gives us an easy way to write the nth power of A



Now, I won't get into proving that this method of diagonalization works. If you want that much detail you can go here. Now, the next step is to find the eigenvectors and eigenvalues of A. So first we'll solve the characteristic equation of A.



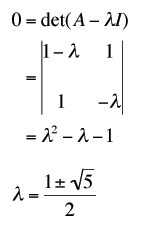
So, now we find the eigenvectors for the two eigenvalues. For the eigenvalue



we find



So our first eigenvalue-eigenvector pair is



Now, for the second eigenvalue



we find



So our second eigenvalue-eigenvector pair is



Now we can construct our matrices



And to calculate P inverse, we'll need the determinant of P (the invese of P is the transpose of the cofactor matrix times one over the determinant)



and so



And now we plug it all in to find a formula for the nth power of A



And so we can see (from our second equation) that the formula for the nth number in the Fibonacci sequence is the lower left entry in this matrix



Using this result, you can easily find a formula for the nth term of any Fibonacci-like sequence (same rules for generating the sequence, but with different starting numbers) just by changing the vector that you multiply with the nth power of A.