Trig Identities

This is a simple trick that helps me remember a number of useful trig identities in one derivation. We'll derive formulas for both cos(A+B) and sin(A+B) at the same time. First we'll derive a useful relationship between the exponential function, sine and cosine. The Taylor expansion of a function is



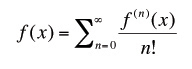
So the Taylor expansion of the the exponential function is



And the Taylor expansion of sine and cosine are



and



Now, expanding the exponential function of i (a square root of -1) times a number theta gives



So, now we'll use the fact that the product of two exponentials is the exponential of the sum of their powers to give



Now given that the real parts of both sides must be equal, as well as the imaginary parts, this one equation yields the following two identities



and



And that wraps her all up. Now you can easily derive cos(2A) and sin(2A) (the double angle identities) by plugging in A for B in the above equations. Similarly, you can derive sin(A-B) and cos(A-B) by substituting -B for B, and remembering that sin(-x) = -sin(x) and cos(-x) = cos(x).