Note : When you refer to an n-sphere, the n refers to the dimension of the manifold, but in this topic, I consider a sphere as a solid (rather than just a manifold), and refer to the manifold as its border. So a 3-dimensional sphere is a ball in R3, rather than the 3-dimensional border of a ball in R4. Sorry for the confusion to all the math majors out there, but I think the average person thinks of a "normal" sphere as a 3-dimensional solid (rather than a 2-dimensional manifold) .. thanks, Andy.
First, let's say that we have a random number generator UnitRand() that generates a uniformly distributed number on the interval [0, 1). Given a generator of random points on the border of a circle, the probability of getting a point whose angle is between 0 and x is
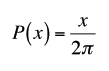
So our random circle point generator needs to be

Now, to get a random point on a sphere, we'll need to derive the surface area of a part of a sphere defined by sweeping a certain angle in longitude and latitude. We'll use this to write a formula for the probability of generating a point in that section, which we'll use to derive a random sphere point generator.
Let's define a function A(r, θ0, ... , θn-1) that is the surface "measure" of a portion of an n-dimensional sphere (1-dimensional sphere is a line segment, 2-dimensional sphere is a circle, etc) subtended by (n-1) ranges of angles (1 for a circle, 2 for a sphere .. longitude and latitude, etc). We know that A(r,θ) = rθ is a formula for the arc length of a circular arc of θ radians and radius r. I'll propose that the formula for the surface area of a portion of a sphere is based off of it

In fact, you can always find the next formula from the previous one by the relation

I won't prove this part (this is going to be long enough already). So, the part of the surface of a sphere swept out by

has the area

With a uniform distribution on the surface of a sphere, the probability of getting a point whose θ1 is between 0 and x is

Therefore the formula for θ1 is

So, a formula for an evenly distributed random point on the surface of a sphere is

Edit: Revised these equations according to a comment pointing out that the original ones were incorrect
Nice proof! However, you've flipped your randomly generated variables in the final result. ie. Theta(1) should be Theta(0)
ReplyDeleteTechnically to make it coherent within your full analysis, (since you identified x(0)=rcos(theta(0)) and x(1)=rsin(theta(0)) as your random circle selection), then your theta(1) terms should be x(0)=sin(theta(1)), x(1)=sin(theta(1)), x(2)=cos(theta(1))
So you're saying that it would make more sense to have
ReplyDeletex_0 = r cos(theta_0) sin(theta_1)
x_1 = r sin(theta_0) sin(theta_1)
x_2 = r cos(theta_1)
Yeah, I think you're right (after looking at it for a while .. it's been a while since I've gone over this stuff).
I'll double check the uniform quaternion stuff to make sure I didn't mess that up in the same way, and then I'll update it. Thanks.
How about:
ReplyDeletedo{
X0=2*UnitRand()-1
X1=2*UnitRand()-1
X2=2*UnitRand()-1
temp=X0*X0+X1*X1+X2*X2
}while (temp>1) OR (temp=0)
temp2=R/sqrt(temp)
X0*=temp2
X1*=temp2
X2*=temp2
No trig at all. Should be super fast. Only down side is you end pick random numbers about twice per point. -Smark
Check out GNU scientific library (http://www.gnu.org/software/gsl/). It has a function for uniform points on the n-dimensional sphere surface.
ReplyDeletewouldn't it be more efficient ("picking random orientations") to just generate two angles ? i mean just and X and Y angle.. and then if needed convert to cartesian, vectors ?
ReplyDeleteIt would be much better if you just stick to the practical physically meaningful sphere rather than generalizing it to n-dimension. If you want to make something accessible, just don't even mention the manifold concept, it would cause more confusion.
ReplyDeleteI came up with the basic approach to a uniform distribution while driving to and from the CAL2010 APS conference. I'm working some code for a cosmic ray sim. It's a brute force method...
ReplyDeletepseudo code...
While(no vector) {
x=, y=, z=... Rand(-1 to 1)
if x^2 +y^2 +z^2 <=1.0, then normalize(x,y,z) and return (x,y,z) or (1,theta,phi) // your choice in the function call
}
The idea is that all points within the "ball" will be a
uniformly distributed and can be projected outward onto the spherical surface. No points outside the sphere can be considered uniform "as projected" because those near the corners of the "box" (+-1,+-1,+-1) will have a greater density when projected down onto the sphere.